The power, over and over again. I must admit that I am thoroughly confused by power calculations for rare genetic variants, particularly for de novo variants that are identified through trio exome sequencing. Carolien has recently written a post about the results we can expect from exome sequencing studies. For a current grant proposal, I have now tried to estimate the rate of de novos using a small simulation experiment. And I have realized that we need to re-think the concept of power.
Power and errors. The idea of statistical power is often used, referring to studies that are “sufficiently powered” to detect difference. However, I always need to think twice when I try to explain this concept to somebody, as it is not easy to grasp. Power has something to do with testing errors and hypotheses, so please give me a minute to review these concepts first. If you don’t feel that you need a review on these topics, please skip to the last sentence of this paragraph. Doing statistics sometimes involves spinning around a countless number of times until you don’t remember anymore where you eventually came from. This, for example, is the case for the p-value. Just imagine you are interested in the height of men and women. Even though you already assume that men are taller than women, statistics require that you turn a blind eye on this. You have to assume that both groups are equally tall (your null hypothesis) only to be surprised that they are not. The level of surprise is your p-value. The critical element in this scenario is the null hypothesis, as you can make two different mistakes pertaining to this. Depending on your criteria, you can reject the null hypothesis even though it’s true (Type I error), i.e. you conclude that men and women differ in size, even though they are equally tall. Alternatively, you might conclude that men and women are equally tall, even though they are not. This is a Type II error. And the Type II error (b) is closely related to the concept of power (1-b). In brief, power is the probability to find a difference if it is actually there. However, if we search for de novo variants in epileptic encephalopathies, what exactly is the difference that are we looking for?
Where is the difference? We have reviewed many of the recent papers on de novo mutations in autism, schizophrenia and intellectual disability and –in a certain way- all these papers convey the same message: every individual, affected or nor, carries between 3-5 de novo variants (“innocent genes”). In patients with neurodevelopmental disorders, some of these variants are causative or contributory to disease (“guilty genes”). How can we tell these two classes apart? On a group level, we would expect a higher frequency of de novo variants in patients with neurodevelopmental disorders or epileptic encephalopathies. However, the recent studies have shown that sample sizes need to be very large to detect this difference, coming back again to the concept of power. A sample size of ~200 trios is probably sufficient to find a difference in frequency of de novo mutations with a p-value of 0.05. Looking through our GWAS goggles, this is troubling. We are used to much more stringent p-values in genetics. If we then include a comparison of mutation subclasses either based on prediction or putative gene function, we will soon run into a multiple testing problem. In addition, these results on a group level don’t tell us anything about the actually genes. Therefore, another criterion is frequently used to assess the role of de novo variants – recurrence. Genes are accepted to be implicated in the etiology of a disease if they are found to be mutated in more than one patient. For example, SCN2A is implicated in autism as several patients with autism were found to have de novo mutations in this gene. Compared to the number of genes found to be mutated, the number of recurrent genes is much smaller. As recurrence instead of group difference appears to be the most straightforward way of judging the role of particular genes, we have to rethink our way of talking about the power of a study.
The null hypothesis, revisited. What is our null hypothesis, what is our p-value for recurrence of de novo mutations in epileptic encephalopathies? The most obvious answer is quite simple. There is no such thing. We don’t compare groups, we don’t perform a statistical test. If we judge the relevance of genes simply by recurrence, we need to address this issue differently. One solution for this is to estimate the number of samples needed to find a gene at least twice.
An issue of architecture. We have tried such an estimation using a small simulation. The ingredients we need for this are (a) the frequency of a given disease variant in patients and (b) the number of genes involved. For our simulation, we assumed that 400 genes contribute to the disease and that each gene has a frequency of 0.2% in the patient population. This, at least to us, might be a reasonable guess for the genetic architecture of the epileptic encephalopathies modeled after what is known in autism: many variants contribute to the disease and mutations within a given gene are rare. Assuming that each of these 400 genes is mutated independently at a frequency of 0.2%, different constellations can be expected. We simulated these constellation 1000 times, each time allowing each gene to be mutated within a patient with a probability of 0.2%. We then counted the number of genes that were mutated at least twice in a cohort of 100 patients (Figure).
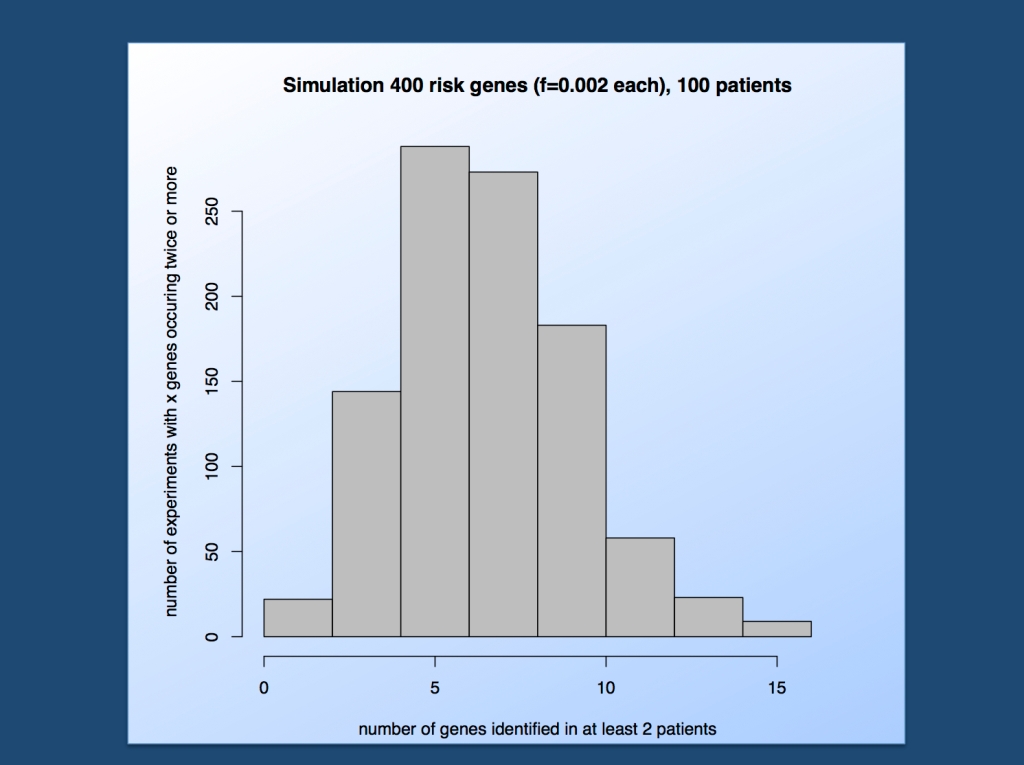
Estimating the number of genes found to be mutated at least twice in patients in epileptic encephalopathies assuming 400 risk genes with a frequency of 0.2% each. In more than 80% of simulations, 5 or more genes will be identified in a cohort of 100 trios.
The bandwidth of possibilities. In summary, the number of genes occurring at least twice has a median of 7. This means, using the parameters outlined above, we expect 7 or more genes to be mutated in at least two patients in most simulations, i.e. of the 400 genes involved, our cohort of 100 patients (actually trios, as we look for de novo variants) will pick up a few. In 80% of experiments, at least 5 genes are found to be recurrent, which may be proxy for the 80% power that is customary in genetic association studies.



